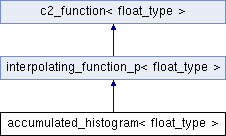
An interpolating_function_p which is the cumulative integral of a histogram.Note than binedges should be one element longer than binheights, since the lower & upper edges are specified. Note that this is a malformed spline, since the second derivatives are all zero, so it has less continuity. Also, note that the bin edges can be given in backwards order to generate the reversed accumulation (starting at the high end) 더 자세히 ...

#include <c2_function.hh>

accumulated_histogram< float_type >에 대한 상속 다이어그램 :

Public 멤버 함수
	accumulated_histogram (const std::vector< float_type >binedges, const std::vector< float_type > binheights, bool normalize=false, bool inverse_function=false, bool drop_zeros=true)
	Construct the integrated histogram. 더 자세히 ...

interpolating_function_p < float_type > &	load (const std::vector< float_type > &x, const std::vector< float_type > &f, bool lowerSlopeNatural, float_type lowerSlope, bool upperSlopeNatural, float_type upperSlope, bool splined=true)
	do the dirty work of constructing the spline from a function. 더 자세히 ...

interpolating_function_p < float_type > &	load_pairs (std::vector< std::pair< float_type, float_type > > &data, bool lowerSlopeNatural, float_type lowerSlope, bool upperSlopeNatural, float_type upperSlope, bool splined=true)
	do the dirty work of constructing the spline from a function. 더 자세히 ...

interpolating_function_p < float_type > &	sample_function (const c2_function< float_type > &func, float_type amin, float_type amax, float_type abs_tol, float_type rel_tol, bool lowerSlopeNatural, float_type lowerSlope, bool upperSlopeNatural, float_type upperSlope)
	do the dirty work of constructing the spline from a function. 더 자세히 ...

interpolating_function_p < float_type > &	load_random_generator_function (const std::vector< float_type > &bincenters, const c2_function< float_type > &binheights)
	initialize from a grid of points and a c2_function (un-normalized) to an interpolator which, when evaluated with a uniform random variate on [0,1] returns random numbers distributed as the input function. 더 자세히 ...

interpolating_function_p < float_type > &	load_random_generator_bins (const std::vector< float_type > &bins, const std::vector< float_type > &binheights, bool splined=true)

virtual float_type	value_with_derivatives (float_type x, float_type yprime, float_type yprime2) const
	get the value and derivatives. 더 자세히 ...

virtual interpolating_function_p < float_type > &	clone () const

void	get_data (std::vector< float_type > &xvals, std::vector< float_type > &yvals) const

void	get_internal_data (std::vector< float_type > &xvals, std::vector< float_type > &yvals, std::vector< float_type > &y2vals) const

void	set_lower_extrapolation (float_type bound)

void	set_upper_extrapolation (float_type bound)

interpolating_function_p < float_type > &	unary_operator (const c2_function< float_type > &source) const

interpolating_function_p < float_type > &	binary_operator (const c2_function< float_type > &rhs, const c2_binary_function< float_type > *combining_stub) const

interpolating_function_p < float_type > &	add_pointwise (const c2_function< float_type > &rhs) const

interpolating_function_p < float_type > &	subtract_pointwise (const c2_function< float_type > &rhs) const

interpolating_function_p < float_type > &	multiply_pointwise (const c2_function< float_type > &rhs) const

interpolating_function_p < float_type > &	divide_pointwise (const c2_function< float_type > &rhs) const

void	clone_data (const interpolating_function_p< float_type > &rhs)

const std::string	cvs_header_vers () const
	get versioning information for the header file 더 자세히 ...

const std::string	cvs_file_vers () const
	get versioning information for the source file 더 자세히 ...

float_type	operator() (float_type x) const
	evaluate the function in the classic way, ignoring derivatives. 더 자세히 ...

float_type	operator() (float_type x, float_type yprime, float_type yprime2) const
	get the value and derivatives. 더 자세히 ...

c2_composed_function_p < float_type > &	operator() (const c2_function< float_type > &inner) const
	compose this function outside another. 더 자세히 ...

float_type	find_root (float_type lower_bracket, float_type upper_bracket, float_type start, float_type value, int error=0, float_type final_yprime=0, float_type *final_yprime2=0) const
	solve f(x)==value very efficiently, with explicit knowledge of derivatives of the function 더 자세히 ...

float_type	partial_integrals (std::vector< float_type > xgrid, std::vector< float_type > *partials=0, float_type abs_tol=1e-12, float_type rel_tol=1e-12, int derivs=2, bool adapt=true, bool extrapolate=true) const

float_type	integral (float_type amin, float_type amax, std::vector< float_type > *partials=0, float_type abs_tol=1e-12, float_type rel_tol=1e-12, int derivs=2, bool adapt=true, bool extrapolate=true) const
	a fully-automated integrator which uses the information provided by the get_sampling_grid() function to figure out what to do. 더 자세히 ...

c2_piecewise_function_p < float_type > *	adaptively_sample (float_type amin, float_type amax, float_type abs_tol=1e-12, float_type rel_tol=1e-12, int derivs=2, std::vector< float_type > xvals=0, std::vector< float_type > yvals=0) const
	create a c2_piecewise_function_p from c2_connector_function_p segments which is a representation of the parent function to the specified accuracy, but maybe much cheaper to evaluate 더 자세히 ...

float_type	xmin () const

float_type	xmax () const

void	set_domain (float_type amin, float_type amax)

size_t	get_evaluations () const

void	reset_evaluations () const
	reset the counter 더 자세히 ...

void	increment_evaluations () const
	count evaluations 더 자세히 ...

bool	check_monotonicity (const std::vector< float_type > &data, const char message[]) const
	check that a vector is monotonic, throw an exception if not, and return a flag if it is reversed 더 자세히 ...

virtual void	set_sampling_grid (const std::vector< float_type > &grid)
	establish a grid of 'interesting' points on the function. 더 자세히 ...

std::vector< float_type > *	get_sampling_grid_pointer () const
	get the sampling grid, which may be a null pointer 더 자세히 ...

virtual void	get_sampling_grid (float_type amin, float_type amax, std::vector< float_type > &grid) const

void	preen_sampling_grid (std::vector< float_type > *result) const
	The grid is modified in place. 더 자세히 ...

void	refine_sampling_grid (std::vector< float_type > &grid, size_t refinement) const

c2_function< float_type > &	normalized_function (float_type amin, float_type amax, float_type norm=1.0) const
	create a new c2_function from this one which is normalized on the interval 더 자세히 ...

c2_function< float_type > &	square_normalized_function (float_type amin, float_type amax, float_type norm=1.0) const

c2_function< float_type > &	square_normalized_function (float_type amin, float_type amax, const c2_function< float_type > &weight, float_type norm=1.0) const
	create a new c2_function from this one which is square-normalized with the provided weight on the interval 더 자세히 ...

c2_sum_p< float_type > &	operator+ (const c2_function< float_type > &rhs) const
	factory function to create a c2_sum_p from a regular algebraic expression. 더 자세히 ...

c2_diff_p< float_type > &	operator- (const c2_function< float_type > &rhs) const
	factory function to create a c2_diff_p from a regular algebraic expression. 더 자세히 ...

c2_product_p< float_type > &	operator* (const c2_function< float_type > &rhs) const
	factory function to create a c2_product_p from a regular algebraic expression. 더 자세히 ...

c2_ratio_p< float_type > &	operator/ (const c2_function< float_type > &rhs) const

float_type	get_trouble_point () const
	Find out where a calculation ran into trouble, if it got a nan. If the most recent computation did not return a nan, this is undefined. 더 자세히 ...

void	claim_ownership () const
	increment our reference count. Destruction is only legal if the count is zero. 더 자세히 ...

size_t	release_ownership_for_return () const
	decrement our reference count. Do not destroy at zero. 더 자세히 ...

void	release_ownership () const

size_t	count_owners () const
	get the reference count, mostly for debugging 더 자세히 ...

void	fill_fblock (c2_fblock< float_type > &fb) const
	fill in a c2_fblock<float_type>... a shortcut for the integrator & sampler 더 자세히 ...

Public 속성
const c2_function_transformation < float_type > &	fTransform

Protected 멤버 함수
void	spline (bool lowerSlopeNatural, float_type lowerSlope, bool upperSlopeNatural, float_type upperSlope)
	create the spline coefficients 더 자세히 ...

virtual void	set_sampling_grid_pointer (std::vector< float_type > &grid)

정적 Protected 멤버 함수
static bool	comp_pair (std::pair< float_type, float_type > const &i, std::pair< float_type, float_type > const &j)

Protected 속성
std::vector< float_type >	Xraw

std::vector< float_type >	X

std::vector< float_type >	F

std::vector< float_type >	y2

c2_const_ptr< float_type >	sampler_function

bool	xInverted

size_t	lastKLow

std::vector< float_type > *	sampling_grid

bool	no_overwrite_grid

float_type	fXMin

float_type	fXMax

size_t	evaluations

float_type	bad_x_point
	this point may be used to record where a calculation ran into trouble 더 자세히 ...

상세한 설명

template<typename float_type = double>
class accumulated_histogram< float_type >

An interpolating_function_p which is the cumulative integral of a histogram.

Note than binedges should be one element longer than binheights, since the lower & upper edges are specified. Note that this is a malformed spline, since the second derivatives are all zero, so it has less continuity. Also, note that the bin edges can be given in backwards order to generate the reversed accumulation (starting at the high end)

c2_function.hh 파일의 2173 번째 라인에서 정의되었습니다.

생성자 & 소멸자 문서화

template<typename float_type = double>

accumulated_histogram< float_type >::accumulated_histogram	(	const std::vector< float_type >	binedges,
		const std::vector< float_type >	binheights,
		bool	normalize = `false`,
		bool	inverse_function = `false`,
		bool	drop_zeros = `true`
	)

Construct the integrated histogram.

매개변수

binedges	the edges of the bins in binheights. It should have one more element than binheights
binheights	the number of counts in each bin.
normalize	if true, normalize integral to 1
inverse_function	if true, drop zero channels, and return inverse function for random generation
drop_zeros	eliminate null bins before integrating, so integral is strictly monotonic.

멤버 함수 문서화

template<typename float_type = double>

c2_piecewise_function_p<float_type>* c2_function< float_type >::adaptively_sample	(	float_type	amin,
		float_type	amax,
		float_type	abs_tol = `1e-12`,
		float_type	rel_tol = `1e-12`,
		int	derivs = `2`,
		std::vector< float_type > *	xvals = `0`,
		std::vector< float_type > *	yvals = `0`
	)		const

inherited

create a c2_piecewise_function_p from c2_connector_function_p segments which is a representation of the parent function to the specified accuracy, but maybe much cheaper to evaluate

This method has three modes, depending on the derivs flag.

If derivs is 2, it computes a c2_piecewise_function_p representation of its parent function, which may be a much faster function to use in codes if the parent function is expensive. If xvals and yvals are non-null, it will also fill them in with the function values at each grid point the adaptive algorithm chooses.

If derivs is 1, this does not create the connectors, and returns an null pointer, but will fill in the xvals and yvals vectors with values of the function at points such that the linear interpolation error between the points is bounded by the tolerance values given. Because it uses derivative information from the function to manage the error control, it is almost completely free of issues with missing periods of oscillatory functions, even with no information provided in the sampling grid. This is typically useful for sampling a function for plotting.

If derivs is 0, this does something very like what it does if derivs = 1, but without derivatives. Instead, to compute the intermediate value of the function for error control, it just uses 3-point parabolic interpolation. This is useful amost exclusively for converting a non-c2_function, with no derivatives, but wrapped in a c2_classic_function wrapper, into a table of values to seed an interpolating_function_p. Note, however, that without derivatives, this is very susceptible to missing periods of oscillatory functions, so it is important to set a sampling grid which isn't too much coarser than the typical oscillations.

주의: the sampling_grid of the returned function matches the sampling_grid of its parent.

참고: Adaptive Sampling Examples

매개변수

	amin	lower bound of the domain for sampling
	amax	upper bound of the domain for sampling
	abs_tol	the absolute error bound for each segment
	rel_tol	the fractional error bound for each segment.
	derivs	if 0 or 1, return a useless function, but fill in the xvals and yvals vectors (if non-null). Also, if 0 or 1, tolerances refer to linear interpolation, not high-order interpolation. If 2, return a full piecewise collection of c2_connector_function_p segments. See discussion above.
[in,out]	xvals	vector of abscissas at which the function was actually sampled (if non-null)
[in,out]	yvals	vector of function values corresponding to xvals (if non-null)

반환값: a new, sampled representation, if derivs is 2. A null pointer if derivs is 0 or 1.

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::add_pointwise ( const c2_function< float_type > & rhs ) const

inlineinherited

c2_function.hh 파일의 1687 번째 라인에서 정의되었습니다.

다음을 참조함 : interpolating_function_p< float_type >::binary_operator().

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::binary_operator	(	const c2_function< float_type > &	rhs,
		const c2_binary_function< float_type > *	combining_stub
	)		const

inherited

다음에 의해서 참조됨 : interpolating_function_p< float_type >::add_pointwise(), interpolating_function_p< float_type >::divide_pointwise(), interpolating_function_p< float_type >::multiply_pointwise(), interpolating_function_p< float_type >::subtract_pointwise().

template<typename float_type = double>

bool c2_function< float_type >::check_monotonicity	(	const std::vector< float_type > &	data,
		const char	message[]
	)		const

inherited

check that a vector is monotonic, throw an exception if not, and return a flag if it is reversed

매개변수

data	a vector of data points which are expected to be monotonic.
message	an informative string to include in an exception if this throws c2_exception

반환값: true if in decreasing order, false if increasing

template<typename float_type = double>

void c2_function< float_type >::claim_ownership ( ) const

inlineinherited

increment our reference count. Destruction is only legal if the count is zero.

c2_function.hh 파일의 506 번째 라인에서 정의되었습니다.

template<typename float_type = double>

virtual interpolating_function_p<float_type>& interpolating_function_p< float_type >::clone ( ) const

inlinevirtualinherited

arrhenius_interpolating_function_p< float_type >, log_log_interpolating_function_p< float_type >, lin_log_interpolating_function_p< float_type >, log_lin_interpolating_function_p< float_type >에서 재구현되었습니다.

c2_function.hh 파일의 1663 번째 라인에서 정의되었습니다.

template<typename float_type = double>

void interpolating_function_p< float_type >::clone_data ( const interpolating_function_p< float_type > & rhs )

inlineinherited

c2_function.hh 파일의 1698 번째 라인에서 정의되었습니다.

다음을 참조함 : interpolating_function_p< float_type >::F, c2_function< float_type >::set_sampling_grid_pointer(), interpolating_function_p< float_type >::X, interpolating_function_p< float_type >::Xraw, interpolating_function_p< float_type >::y2.

template<typename float_type = double>

static bool interpolating_function_p< float_type >::comp_pair	(	std::pair< float_type, float_type > const &	i,
		std::pair< float_type, float_type > const &	j
	)

inlinestaticprotectedinherited

c2_function.hh 파일의 1712 번째 라인에서 정의되었습니다.

template<typename float_type = double>

size_t c2_function< float_type >::count_owners ( ) const

inlineinherited

get the reference count, mostly for debugging

반환값: the count

c2_function.hh 파일의 524 번째 라인에서 정의되었습니다.

template<typename float_type = double>

const std::string c2_function< float_type >::cvs_file_vers ( ) const

inherited

get versioning information for the source file

반환값: the CVS Id string

template<typename float_type = double>

const std::string c2_function< float_type >::cvs_header_vers ( ) const

inlineinherited

get versioning information for the header file

반환값: the CVS Id string

c2_function.hh 파일의 151 번째 라인에서 정의되었습니다.

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::divide_pointwise ( const c2_function< float_type > & rhs ) const

inlineinherited

c2_function.hh 파일의 1696 번째 라인에서 정의되었습니다.

다음을 참조함 : interpolating_function_p< float_type >::binary_operator().

template<typename float_type = double>

void c2_function< float_type >::fill_fblock ( c2_fblock< float_type > & fb ) const

inlineinherited

fill in a c2_fblock<float_type>... a shortcut for the integrator & sampler

매개변수

[in,out] fb the block to fill in with information

c2_function.hh 파일의 556 번째 라인에서 정의되었습니다.

template<typename float_type = double>

float_type c2_function< float_type >::find_root	(	float_type	lower_bracket,
		float_type	upper_bracket,
		float_type	start,
		float_type	value,
		int *	error = `0`,
		float_type *	final_yprime = `0`,
		float_type *	final_yprime2 = `0`
	)		const

inherited

solve f(x)==value very efficiently, with explicit knowledge of derivatives of the function

find_root solves by iterated inverse quadratic extrapolation for a solution to f(x)=y. It includes checks against bad convergence, so it should never be able to fail. Unlike typical secant method or fancier Brent's method finders, this does not depend in any strong wasy on the brackets, unless the finder has to resort to successive approximations to close in on a root. Often, it is possible to make the brackets equal to the domain of the function, if there is any clue as to where the root lies, as given by the parameter start.

매개변수

	lower_bracket	the lower bound for the search
	upper_bracket	the upper bound for the search. Function sign must be opposite to that at lower_bracket
	start	starting value for the search
	value	the value of the function being sought (solves f(x) = value)
[out]	error	If pointer is zero, errors raise exception. Otherwise, returns error here.
[out]	final_yprime	If pointer is not zero, return derivative of function at root
[out]	final_yprime2	If pointer is not zero, return second derivative of function at root

반환값: the position of the root.

참고: Root finding sample

다음에 의해서 참조됨 : G4ScreenedCoulombClassicalKinematics::DoScreeningComputation().

template<typename float_type = double>

void interpolating_function_p< float_type >::get_data	(	std::vector< float_type > &	xvals,
		std::vector< float_type > &	yvals
	)		const

inherited

template<typename float_type = double>

size_t c2_function< float_type >::get_evaluations ( ) const

inlineinherited

and sampler do increment it.

반환값: number of evaluations logged since last reset.

c2_function.hh 파일의 395 번째 라인에서 정의되었습니다.

template<typename float_type = double>

void interpolating_function_p< float_type >::get_internal_data	(	std::vector< float_type > &	xvals,
		std::vector< float_type > &	yvals,
		std::vector< float_type > &	y2vals
	)		const

inlineinherited

c2_function.hh 파일의 1670 번째 라인에서 정의되었습니다.

다음을 참조함 : interpolating_function_p< float_type >::F, interpolating_function_p< float_type >::X, interpolating_function_p< float_type >::y2.

template<typename float_type = double>

virtual void c2_function< float_type >::get_sampling_grid	(	float_type	amin,
		float_type	amax,
		std::vector< float_type > &	grid
	)		const

virtualinherited

c2_sin_p< float_type >, c2_plugin_function_p< float_type >, c2_plugin_function_p< G4double >에서 재구현되었습니다.

다음에 의해서 참조됨 : c2_plugin_function_p< G4double >::get_sampling_grid().

template<typename float_type = double>

std::vector<float_type>* c2_function< float_type >::get_sampling_grid_pointer ( ) const

inlineinherited

get the sampling grid, which may be a null pointer

반환값: pointer to the sampling grid

c2_function.hh 파일의 432 번째 라인에서 정의되었습니다.

template<typename float_type = double>

float_type c2_function< float_type >::get_trouble_point ( ) const

inlineinherited

Find out where a calculation ran into trouble, if it got a nan. If the most recent computation did not return a nan, this is undefined.

반환값: x value of point at which something went wrong, if integrator (or otherwise) returned a nan.

c2_function.hh 파일의 502 번째 라인에서 정의되었습니다.

template<typename float_type = double>

void c2_function< float_type >::increment_evaluations ( ) const

inlineinherited

count evaluations

c2_function.hh 파일의 399 번째 라인에서 정의되었습니다.

다음에 의해서 참조됨 : c2_function< G4double >::fill_fblock().

template<typename float_type = double>

float_type c2_function< float_type >::integral	(	float_type	amin,
		float_type	amax,
		std::vector< float_type > *	partials = `0`,
		float_type	abs_tol = `1e-12`,
		float_type	rel_tol = `1e-12`,
		int	derivs = `2`,
		bool	adapt = `true`,
		bool	extrapolate = `true`
	)		const

inherited

a fully-automated integrator which uses the information provided by the get_sampling_grid() function to figure out what to do.

It returns the integral of the function over the domain requested with error tolerances as specified. It is just a front-end to partial_integrals()

매개변수

amin	lower bound of the domain for integration
amax	upper bound of the domain for integration
partials	if non-NULL, a vector in which to receive the partial integrals. It will automatically be sized appropriately, if provided, to contain n - 1 elements where n is the length of xgrid
abs_tol	the absolute error bound for each segment
rel_tol	the fractional error bound for each segment. If the error is smaller than either the relative or absolute tolerance, the integration step is finished.
derivs	number of derivatives to trust, which sets the order of the integrator. The order is 3*derivs + 4. derivs can be 0, 1, or 2.
adapt	if true, use recursive adaptation, otherwise do simple evaluation on the grid provided with no error checking.
extrapolate	if true, use simple Richardson extrapolation on the final 2 steps to reduce the error.

반환값: sum of partial integrals, which is the definite integral from the first value in xgrid to the last.

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::load	(	const std::vector< float_type > &	x,
		const std::vector< float_type > &	f,
		bool	lowerSlopeNatural,
		float_type	lowerSlope,
		bool	upperSlopeNatural,
		float_type	upperSlope,
		bool	splined = `true`
	)

inherited

do the dirty work of constructing the spline from a function.

매개변수

x	the list of abscissas. Must be either strictly increasing or strictly decreasing. Strictly increasing is preferred, as less memory is used since a copy is not required for the sampling grid.
f	the list of function values.
lowerSlopeNatural	if true, set y''(first point)=0, otherwise compute it from lowerSope
lowerSlope	derivative of the function at the lower bound, used only if lowerSlopeNatural is false
upperSlopeNatural	if true, set y''(last point)=0, otherwise compute it from upperSope
upperSlope	derivative of the function at the upper bound, used only if upperSlopeNatural is false
splined	if true (default), use cubic spline, if false, use linear interpolation.

반환값: the same interpolating function, filled

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::load_pairs	(	std::vector< std::pair< float_type, float_type > > &	data,
		bool	lowerSlopeNatural,
		float_type	lowerSlope,
		bool	upperSlopeNatural,
		float_type	upperSlope,
		bool	splined = `true`
	)

inherited

do the dirty work of constructing the spline from a function.

매개변수

data	std::vector of std::pairs of x,y. Will be sorted into x increasing order in place.
lowerSlopeNatural	if true, set y''(first point)=0, otherwise compute it from lowerSope
lowerSlope	derivative of the function at the lower bound, used only if lowerSlopeNatural is false
upperSlopeNatural	if true, set y''(last point)=0, otherwise compute it from upperSope
upperSlope	derivative of the function at the upper bound, used only if upperSlopeNatural is false
splined	if true (default), use cubic spline, if false, use linear interpolation.

반환값: the same interpolating function, filled

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::load_random_generator_bins	(	const std::vector< float_type > &	bins,
		const std::vector< float_type > &	binheights,
		bool	splined = `true`
	)

inherited

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::load_random_generator_function	(	const std::vector< float_type > &	bincenters,
		const c2_function< float_type > &	binheights
	)

inherited

initialize from a grid of points and a c2_function (un-normalized) to an interpolator which, when evaluated with a uniform random variate on [0,1] returns random numbers distributed as the input function.

참고: Arbitrary random generation inverse_integrated_density starts derivatives a probability density std::vector, generates the integral, and generates an interpolating_function_p of the inverse function which, when evaluated using a uniform random on [0,1] returns values derivatives a density distribution equal to the input distribution If the data are passed in reverse order (large X first), the integral is carried out from the big end.

매개변수

bincenters	the positions at which to sample the function binheights
binheights	a function which describes the density of the random number distribution to be produced.

반환값: an initialized interpolator, which if evaluated randomly with a uniform variate on [0,1] produces numbers distributed according to binheights

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::multiply_pointwise ( const c2_function< float_type > & rhs ) const

inlineinherited

c2_function.hh 파일의 1693 번째 라인에서 정의되었습니다.

다음을 참조함 : interpolating_function_p< float_type >::binary_operator().

template<typename float_type = double>

c2_function<float_type>& c2_function< float_type >::normalized_function	(	float_type	amin,
		float_type	amax,
		float_type	norm = `1.0`
	)		const

inherited

create a new c2_function from this one which is normalized on the interval

매개변수

amin	lower bound of the domain for integration
amax	upper bound of the domain for integration
norm	the desired integral for the function over the region

반환값: a new c2_function with the desired norm.

template<typename float_type = double>

float_type c2_function< float_type >::operator() ( float_type x ) const

inlineinherited

evaluate the function in the classic way, ignoring derivatives.

매개변수

x	the point at which to evaluate

반환값: the value of the function

c2_function.hh 파일의 186 번째 라인에서 정의되었습니다.

template<typename float_type = double>

float_type c2_function< float_type >::operator()	(	float_type	x,
		float_type *	yprime,
		float_type *	yprime2
	)		const

inlineinherited

get the value and derivatives.

매개변수

[in]	x	the point at which to evaluate the function
[out]	yprime	the first derivative (if pointer is non-null)
[out]	yprime2	the second derivative (if pointer is non-null)

반환값: the value of the function

c2_function.hh 파일의 195 번째 라인에서 정의되었습니다.

template<typename float_type = double>

c2_composed_function_p<float_type>& c2_function< float_type >::operator() ( const c2_function< float_type > & inner ) const

inlineinherited

compose this function outside another.

매개변수

inner the inner function

반환값: the composed function

c2_function.hh 파일의 495 번째 라인에서 정의되었습니다.

template<typename float_type = double>

c2_product_p<float_type>& c2_function< float_type >::operator* ( const c2_function< float_type > & rhs ) const

inlineinherited

factory function to create a c2_product_p from a regular algebraic expression.

매개변수

rhs	the right-hand term of the product

반환값: a new c2_function

c2_function.hh 파일의 486 번째 라인에서 정의되었습니다.

template<typename float_type = double>

c2_sum_p<float_type>& c2_function< float_type >::operator+ ( const c2_function< float_type > & rhs ) const

inlineinherited

factory function to create a c2_sum_p from a regular algebraic expression.

매개변수

rhs	the right-hand term of the sum

반환값: a new c2_function

c2_function.hh 파일의 473 번째 라인에서 정의되었습니다.

template<typename float_type = double>

c2_diff_p<float_type>& c2_function< float_type >::operator- ( const c2_function< float_type > & rhs ) const

inlineinherited

factory function to create a c2_diff_p from a regular algebraic expression.

매개변수

rhs	the right-hand term of the difference

반환값: a new c2_function

c2_function.hh 파일의 479 번째 라인에서 정의되었습니다.

template<typename float_type = double>

c2_ratio_p<float_type>& c2_function< float_type >::operator/ ( const c2_function< float_type > & rhs ) const

inlineinherited

c2_function.hh 파일의 488 번째 라인에서 정의되었습니다.

template<typename float_type = double>

float_type c2_function< float_type >::partial_integrals	(	std::vector< float_type >	xgrid,
		std::vector< float_type > *	partials = `0`,
		float_type	abs_tol = `1e-12`,
		float_type	rel_tol = `1e-12`,
		int	derivs = `2`,
		bool	adapt = `true`,
		bool	extrapolate = `true`
	)		const

inherited

solve f(x)=value partial_integrals uses a method with an error O(dx**10) with full information from the derivatives, and falls back to lower order methods if informed of incomplete derivatives. It uses exact midpoint splitting of the intervals for recursion, resulting in no recomputation of the function during recursive descent at previously computed points.

매개변수

xgrid	points between which to evaluate definite integrals.
partials	if non-NULL, a vector in which to receive the partial integrals. It will automatically be sized apprpropriately, if provided, to contain n - 1 elements where n is the length of xgrid
abs_tol	the absolute error bound for each segment
rel_tol	the fractional error bound for each segment. If the error is smaller than either the relative or absolute tolerance, the integration step is finished.
derivs	number of derivatives to trust, which sets the order of the integrator. The order is 3*derivs + 4. derivs can be 0, 1, or 2.
adapt	if true, use recursive adaptation, otherwise do simple evaluation on the grid provided with no error checking.
extrapolate	if true, use simple Richardson extrapolation on the final 2 steps to reduce the error.

반환값: sum of partial integrals, which is the definite integral from the first value in xgrid to the last.

template<typename float_type = double>

void c2_function< float_type >::preen_sampling_grid ( std::vector< float_type > * result ) const

inherited

The grid is modified in place.

template<typename float_type = double>

void c2_function< float_type >::refine_sampling_grid	(	std::vector< float_type > &	grid,
		size_t	refinement
	)		const

inherited

template<typename float_type = double>

void c2_function< float_type >::release_ownership ( ) const

inlineinherited

c2_function.hh 파일의 519 번째 라인에서 정의되었습니다.

template<typename float_type = double>

size_t c2_function< float_type >::release_ownership_for_return ( ) const

inlineinherited

decrement our reference count. Do not destroy at zero.

반환값: final owner count, to check whether object should disappear.

c2_function.hh 파일의 509 번째 라인에서 정의되었습니다.

다음에 의해서 참조됨 : c2_function< G4double >::release_ownership().

template<typename float_type = double>

void c2_function< float_type >::reset_evaluations ( ) const

inlineinherited

reset the counter

c2_function.hh 파일의 397 번째 라인에서 정의되었습니다.

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::sample_function	(	const c2_function< float_type > &	func,
		float_type	amin,
		float_type	amax,
		float_type	abs_tol,
		float_type	rel_tol,
		bool	lowerSlopeNatural,
		float_type	lowerSlope,
		bool	upperSlopeNatural,
		float_type	upperSlope
	)

inherited

do the dirty work of constructing the spline from a function.

매개변수

func	a function without any requirement of valid derivatives to sample into an interpolating function. Very probably a c2_classic_function.
amin	the lower bound of the region to sample
amax	the upper bound of the region to sample
abs_tol	the maximum absolute error permitted when linearly interpolating the points. the real error will be much smaller, since this uses cubic splines at the end.
rel_tol	the maximum relative error permitted when linearly interpolating the points. the real error will be much smaller, since this uses cubic splines at the end.
lowerSlopeNatural	if true, set y'(first point) from 3-point parabola, otherwise compute it from lowerSope
lowerSlope	derivative of the function at the lower bound, used only if lowerSlopeNatural is false
upperSlopeNatural	if true, set y'(last point) from 3-point parabola, otherwise compute it from upperSope
upperSlope	derivative of the function at the upper bound, used only if upperSlopeNatural is false

반환값: the same interpolating function, filled

주의: If the interpolator being filled has a log vertical axis, put the desired relative error in abs_tol, and 0 in rel_tol since the absolute error on the log of a function is the relative error on the function itself.

template<typename float_type = double>

void c2_function< float_type >::set_domain	(	float_type	amin,
		float_type	amax
	)

inlineinherited

c2_function.hh 파일의 391 번째 라인에서 정의되었습니다.

다음에 의해서 참조됨 : c2_binary_function< float_type >::c2_binary_function(), c2_composed_function_p< float_type >::c2_composed_function_p(), LJZBLScreening(), c2_plugin_function_p< G4double >::set_function().

template<typename float_type = double>

void interpolating_function_p< float_type >::set_lower_extrapolation ( float_type bound )

inherited

template<typename float_type = double>

virtual void c2_function< float_type >::set_sampling_grid ( const std::vector< float_type > & grid )

virtualinherited

establish a grid of 'interesting' points on the function.

The sampling grid describes a reasonable initial set of points to look at the function. this should generally be set at a scale which is quite coarse, and sufficient for initializing adaptive integration or possibly root bracketing. For sampling a function to build a new interpolating function, one may want to refine this for accuracy. However, interpolating_functions themselves return their original X grid by default, so refining the grid in this case might be a bad idea.

매개변수

grid	a vector of abscissas. The contents is copied into an internal vector, so the grid can be discarded after passingin.

template<typename float_type = double>

virtual void c2_function< float_type >::set_sampling_grid_pointer ( std::vector< float_type > & grid )

inlineprotectedvirtualinherited

c2_function.hh 파일의 538 번째 라인에서 정의되었습니다.

다음에 의해서 참조됨 : interpolating_function_p< float_type >::clone_data().

template<typename float_type = double>

void interpolating_function_p< float_type >::set_upper_extrapolation ( float_type bound )

inherited

template<typename float_type = double>

void interpolating_function_p< float_type >::spline	(	bool	lowerSlopeNatural,
		float_type	lowerSlope,
		bool	upperSlopeNatural,
		float_type	upperSlope
	)

protectedinherited

create the spline coefficients

template<typename float_type = double>

c2_function<float_type>& c2_function< float_type >::square_normalized_function	(	float_type	amin,
		float_type	amax,
		float_type	norm = `1.0`
	)		const

inherited

template<typename float_type = double>

c2_function<float_type>& c2_function< float_type >::square_normalized_function	(	float_type	amin,
		float_type	amax,
		const c2_function< float_type > &	weight,
		float_type	norm = `1.0`
	)		const

inherited

create a new c2_function from this one which is square-normalized with the provided weight on the interval

매개변수

amin	lower bound of the domain for integration
amax	upper bound of the domain for integration
weight	a c2_function providing the weight
norm	the desired integral for the function over the region

반환값: a new c2_function with the desired norm.

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::subtract_pointwise ( const c2_function< float_type > & rhs ) const

inlineinherited

c2_function.hh 파일의 1690 번째 라인에서 정의되었습니다.

다음을 참조함 : interpolating_function_p< float_type >::binary_operator().

template<typename float_type = double>

interpolating_function_p<float_type>& interpolating_function_p< float_type >::unary_operator ( const c2_function< float_type > & source ) const

inherited

template<typename float_type = double>

virtual float_type interpolating_function_p< float_type >::value_with_derivatives	(	float_type	x,
		float_type *	yprime,
		float_type *	yprime2
	)		const

virtualinherited

get the value and derivatives.

There is required checking for null pointers on the derivatives, and most implementations should operate faster if derivatives are not

매개변수

[in]	x	the point at which to evaluate the function
[out]	yprime	the first derivative (if pointer is non-null)
[out]	yprime2	the second derivative (if pointer is non-null)